Description of the project

Practical Competitive Prediction

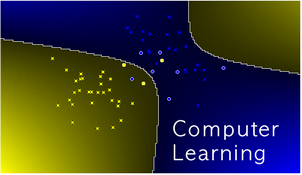
Project Description

The problem of prediction is central in many areas of science, and various general methods of prediction have been developed in machine learning, statistics, and other areas of applied mathematics. Our research project is in the machine-learning tradition.

A common feature of the standard methods of prediction is their reliance on various stochastic assumptions made about the data-generating mechanism. For example, the currently dominant approach to prediction in machine learning is statistical learning theory. This theory gives interesting and useful performance guarantees for various prediction algorithms but makes a restrictive assumption on the way the data are generated: they are assumed to consist of independent and identically distributed labelled instances. Other possible assumptions are the stationarity or the Gaussian distribution of the data sequence.

Competitive prediction does not make any assumptions on data generation but still produces strong performance guarantees in the on-line prediction framework; in many cases, these guarantees are as strong as those obtained in statistical learning theory. The role of stochastic assumptions is played by a benchmark class of prediction strategies: the predictor first decides what class of prediction strategies he or she wants to compete with, and methods of competitive prediction produce predictions whose cumulative loss does not exceed the loss of any prediction strategy in the benchmark class plus a small overhead term. The task of competitive prediction is to design efficient algorithms that minimize the overhead term.

An important development in machine learning in recent years has been the explosion of interest in kernel methods (started by Vapnik's invention of support vector machines). The so-called "kernel trick" allows one to apply linear methods to non-linear problems. The kernel trick has been applied to several algorithms of competitive prediction to obtain competitive loss bounds for benchmark classes that are Hilbert spaces of prediction strategies (basically, classes of prediction strategies that are equipped with the notion of scalar product). The prediction algorithms themselves work with kernels rather than Hilbert spaces directly, which makes them computationally efficient. Since a large number of kernels have been developed for various applications, such as pattern recognition, web, bioinformatics, linguistics, etc., this makes the methods of competitive prediction very widely applicable.

The Hilbert spaces form a relatively small subclass of the Banach spaces, and the main goal of this project is to develop methods of competitive prediction for benchmark classes of prediction strategies that form Banach rather than Hilbert spaces. Why is this important? For us there are two main reasons.

The overhead term in the competitive loss bounds involves the norm of the prediction strategy in the benchmark class we are competing with. Therefore, norm of prediction strategies plays a fundamental role in competitive prediction, whereas scalar product appears extraneous (albeit important for some algorithms and methods of their analysis).

From the pragmatic point of view, Banach function spaces provide many new interesting and practically important examples of benchmark classes of prediction strategies. For example, some benchmark classes are just too big to be equipped with scalar product. We believe that Banach-space methods have potential to extend further the domain of applicability of competitive prediction.